minfc.hh File Reference

#include "Functions.hh"

Include dependency graph for minfc.hh:

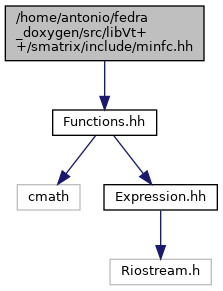
Go to the source code of this file.

Functions
template<class T , class P >
bool	Rminfc (T(*f)(P), P a, P b, double eps, double delta, P &x, P &y)
template<class C , class T , class P >
bool	RminfcM (const C &part, T(C::*f)(P) const, P a, P b, double eps, double delta, P &x, P &y)

Function Documentation

Rminfc()

template<class T , class P >

bool Rminfc	(	T(*)(P)	f,
		P	a,
		P	b,
		double	eps,
		double	delta,
		P &	x,
		P &	y
	)

Rminfc. Function which finds a single, local minimum of a function with one variable in a given interval. The "golden section search" is applied. The method uses a fixed number $n$ of function evaluations, where $n = [2.08\cdot\ln(|a-b|/\epsilon)+1/2] + 1$.

Parameters

f	one-dimensional function
a,b	end-points of search interval
eps	accuracy parameter $\epsilon$
delta	tolerance interval $\delta$ near $a$ and $b$. Suggested value: $\delta = 10\epsilon$
x	computed approximation to the abscissa of a minimum of the function $f$
y	value of $f(x)$

                                                                        {
 
  // Local variables
  static P c, d, h;
  static int n;
  static P v, w, fv, fw;
  bool lge = true, llt = true;
  
 
  n = -1;
  if (a != b) {
    n = round(log(fabs(a - b) / eps) * 2.08);
  }
  c = a;
  d = b;
  if (a > b) {
    c = b;
    d = a;
  }
 
  do {
    h = d - c;
    if (llt == true) {
      v = c + h * 0.3819660112501051;
      fv = (*f)(v);
    }
    if (lge == true) {
      w = c + h * 0.6180339887498949;
      fw = (*f)(w);
    }
    if (fv < fw) {
      llt = true;
      lge = false;
      d = w;
      w = v;
      fw = fv;
    } else {
      llt = false;
      lge = true;
      c = v;
      v = w;
      fv = fw;
    }
    --n;
  } while (n >= 0);
 
  x = (c + d) * .5;
  y = (*f)(x);
  return (fabs(x - a) > delta) && (fabs(x - b) > delta);
} // Rminfc

RminfcM()

template<class C , class T , class P >

bool RminfcM	(	const C &	part,
		T(C::*)(P) const	f,
		P	a,
		P	b,
		double	eps,
		double	delta,
		P &	x,
		P &	y
	)

RminfcM. Rminfc version for const class member functions.

Function which finds a single, local minimum of a function with one variable in a given interval. The "golden section search" is applied. The method uses a fixed number $n$ of function evaluations, where $n = [2.08\cdot\ln(|a-b|/\epsilon)+1/2] + 1$.

Parameters

f	one-dimensional function
a,b	end-points of search interval
eps	accuracy parameter $\epsilon$
delta	tolerance interval $\delta$ near $a$ and $b$. Suggested value: $\delta = 10\epsilon$
x	computed approximation to the abscissa of a minimum of the function $f$
y	value of $f(x)$

                                                                                              {
 
  // Local variables
  static P c, d, h;
  static int n;
  static P v, w, fv, fw;
  bool lge = true, llt = true;
  
 
  n = -1;
  if (a != b) {
    n = round(log(fabs(a - b) / eps) * 2.08);
  }
  c = a;
  d = b;
  if (a > b) {
    c = b;
    d = a;
  }
 
  do {
    h = d - c;
    if (llt == true) {
      v = c + h * 0.3819660112501051;
      fv = (part.*f)(v);
    }
    if (lge == true) {
      w = c + h * 0.6180339887498949;
      fw = (part.*f)(w);
    }
    if (fv < fw) {
      llt = true;
      lge = false;
      d = w;
      w = v;
      fw = fv;
    } else {
      llt = false;
      lge = true;
      c = v;
      v = w;
      fv = fw;
    }
    --n;
  } while (n >= 0);
 
  x = (c + d) * .5;
  y = (part.*f)(x);
  return (fabs(x - a) > delta) && (fabs(x - b) > delta);
} // Rminfc